Bernhard Meirose is an associate professor (docent) at Lund University and a researcher at Stockholm University. He holds a doctorate from the Federal University of Rio de Janeiro in Brazil and has previously worked as a postdoctoral researcher at CERN and Freiburg University in Germany. He also worked at the University of Texas in Dallas as a research scientist and adjunct lecturer (USA). His research focuses on particle physics, both experimental and phenomenological.
Bernhard was a member of the ATLAS Collaboration from 2007 until 2021, working on a variety of topics in the field, including physics analysis, detector and Monte Carlo simulation, and methods for particle reconstruction and identification. Between 2014 and 2018, he oversaw the hunt for quick dark photons. He was one of the co-proposers of the NNBAR experiment at the European Spallation Source in 2014, and in January 2021, he was named detector simulation coordinator of the experiment.
Last November, I had the good fortune of running with Bernhard in the KLM lounge at Amsterdam Airport while waiting for my trip. I didn’t recognize him, but when I noticed his laptop screen, which was showing a slide from the GEANT4 software, I approached him and asked, “Hi, are you a particle physicist?” “Yes, are you Tommaso?” he said, raising his eyes from the TV and looking at me. Bernhard, it turns out, reads my blog. After a lively debate, we decided that he would contribute a piece to this column about his fascinating findings.
He supplied the following paragraph as an example. Bernhard, thank you very much!
You’ve probably heard about neutrons, whether or not you’re a professional scientist. Neutrons are found in all atoms in nature, with the exception of the most prevalent hydrogen isotope. A free neutron is inherently unstable, decaying spontaneously to a proton, an electron, and an antineutrino in little under 15 minutes on average. A free neutron has long been thought to be capable of doing something quite extraordinary before decaying – converting to antimatter (an antineutron). To look for this, we may now create a high precision experiment (HIBEAM/NNBAR). This is a one-of-a-kind experiment with a one-of-a-kind observable and capability that is part of a larger global program of experiments, each turning over its own rock in search of baryon number violation. Any detection of this magnitude would be comparable to the finding of the Higgs particle. Our experiment yielded a 1000-fold increase in sensitivity above the previous record. In particle physics investigations, such an increase in sensitivity is uncommon.
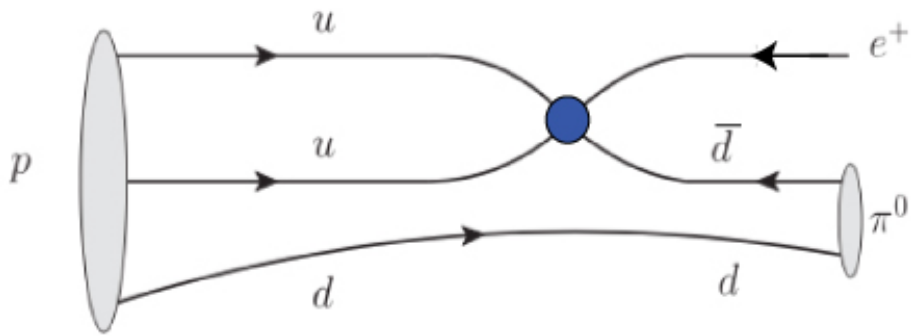
It’s helpful to think about protons in order to grasp the concept of baryon number violation. Free neutrons are known to decay. What about protons, for example? As seen in Figure 1, protons can decay into a neutral pion and a positron (the positively charged twin of the electron): There’s just one issue with it. Nobody has ever witnessed a proton decompose into something (you can see for yourself in Wikipedia that “proton decay” is on the list of the most important unsolved problems in physics). As a result, despite years of experimentation, no one has ever seen proton decay. If protons decay, they must do so after 1034 years, according to the current best limit from the Super-Kamiokande water Cherenkov radiation detector in Japan. This finding was acquired by watching a huge number of protons for a quantifiable amount of time and confirming that no protons ever decayed, given that the estimated age of the Universe is on the order of 1010 years. So, if protons don’t decay, what is the mechanism that keeps them from doing so?
Figure 1. A free proton decaying into a positron and a neutral pion (long sought but never observed).
Protons do not decay, according to the Standard Model of particle physics, since they must conserve a quantity termed “baryon number,” which was initially proposed in 1929 by German theoretical physicist and mathematician Hermann Weyl in order to “explain” the non-observation of proton decay. Any composite state containing three quarks is referred to as a baryon. With one unit of baryonic number (B = 1), the proton is the lightest baryon and cannot decay into anything else. Because neither pions nor protons are baryons, the decay I outlined before (neutral pion and positron) would violate the total baryon number because the system’s ultimate baryon number would be zero. I trust you saw my skepticism in placing the word “explain” in quotation marks because nothing has been explained (we could have called it “Smurf number” and ended up at the same conclusion). Whether I or anybody else likes it or not, baryon number conservation has remained constant, and no experiment has ever shown a breach of it. I’m not sure I’d care if it was only for the sake of learning about proton lifespan. The idea of baryon number violation, on the other hand, lies at the center of some of modern physics’ most basic unanswered issues.
The apparent imbalance between matter (baryons, B = 1) and antimatter (antibaryons, B = – 1) in the Universe is an outstanding challenge in physics. The issue is that matter and antimatter annihilate, creating photons (the particles that make up light), yet matter and antimatter should have been generated in equal numbers, according to the Big Bang hypothesis. However, we do not witness this; the Universe is not formed entirely of light, and there are more baryons than antibaryons. To answer the riddle, Soviet physicist Andrei Sakharov established three requirements in 1967 to describe the process that leads to baryonic matter domination over antibaryonic matter, known as “baryogenesis.” If you’re interested, you can check up all of the prerequisites, but I’ll just state that baryon number violation is one of them – in other words, the condition is required (but not sufficient) to explain baryogenesis.
What about particle physics’ Standard Model? The Standard Model is based on conservation rules known as symmetry. Not all conservation regulations, however, are created equal. The Standard Model, for example, strongly supports electric charge conservation since it corresponds to a gauge symmetry, which is one of the theory’s engines. A so-called accident symmetry causes baryon number conservation. It wasn’t expressly written into the model as a guiding concept, but it does show up after it’s put together. Physicists’ Great Game is to think beyond the Standard Model. Although new theories must maintain the extremely successful engine (theorists do not want to forecast electric charge non-conservation), baryon number conservation tends to disappear when the Standard Model is broadened.
The stakes are huge, given all that baryon number violation may explain and illustrate. Furthermore, given the haphazard nature of the initial rationale for baryon number conservation postulation, I’m not holding my breath that it will hold. In fact, I’m betting it will be violated at some point in the future (if I’m lucky, during my lifetime). And the easiest way to see if the baryon number is broken is to perform a free neutron oscillation, which is a type of proton decay experiment. When I say “cleanly,” I’m referring to a procedure in which just the baryon number is violated. The baryon number is broken in proton decay tests, but the difficulty is that the lepton number (another additive quantum number similar to the baryon number, but for leptons such as electrons and muons) is also violated (since there is no lepton in the initial state but there is a lepton, the positron, in the final state). But what is a neutron oscillation precisely, and how can we detect one?
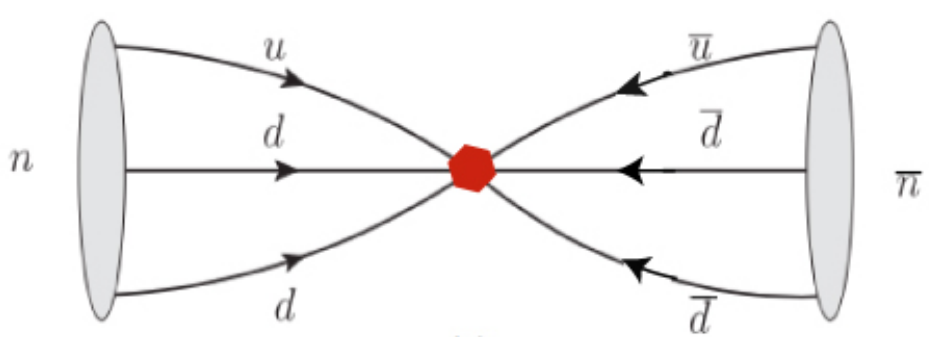
Figure 2. A neutron spontaneously transforming into an antineutron.
A neutron (baryon) can spontaneously transition into an antineutron (antibaryon) in a neutron oscillation, as illustrated in Figure 2, and this can happen back and forth, thus it can oscillate between the two states. Only the baryon number is broken since no other quantum numbers are involved. A significant number of neutrons must be allowed to fly freely for as long as possible in order to enhance the likelihood of at least one neutron changing into an antineutron.
Similar to how you raise your chances of winning the lottery by purchasing more tickets, increasing the number of particles increases your chances of witnessing a rare process (if it exists, it must be uncommon, else it would already have been detected). Furthermore, by studying each neutron for as long as possible, you improve your chances of witnessing the process, therefore you want both free and slow flying neutrons.
With the installation of the European Spallation Source in Lund, Sweden (shown in Figure 3), ideal circumstances for this measurement arose. The facility is now under development, and when completed, it will be the world’s most powerful neutron source, with an unparalleled quantity of neutrons accessible. A 200-meter fly route is also available, as well as unique moderator technology (moderators slow down fast neutrons). The combination of all of these advances makes a free neutron oscillation experiment at the ESS a thousand times more sensitive to detect a neutron oscillation than the previous free neutron oscillation experiment, which was conducted in the 1990s at the Institute Laue-Langevin in France. The NNBAR worldwide partnership was formed as a result of this once-in-a-lifetime scientific opportunity. The team recommends that the experiment be built at the European Spallation Source, with data collection commencing around 2030.
Figure 3. Aerial view over ESS site January 2021
Another point to mention is that in order to observe an antineutron, one must be able to measure its annihilation products, which necessitates placing a suitable material in the path of neutrons with a high probability of antineutron annihilation in the event of a neutron to antineutron transformation. This is done with carbon, where an antineutron is projected to destroy over 100 percent of the time. When an antineutron collides with one of the carbon neutrons, numerous pions are produced, which must be collected by a detector around it. The proof would be clear and compelling: charged and neutron pions both originate from the same point (vertex), and the masses and energy of all pions should total up to two neutron masses when added together (one for the neutron in the carbon, the other for the antineutron). Figure 4 depicts the experiment’s layout.
And what does the discovery of the baryon number imply? The observation of baryon number violation in free neutron oscillations would be the first evidence of non-Standard Model physics beyond the neutrino sector, in addition to fulfilling one of Sakharov’s conditions and shedding light on one of modern cosmology’s most pressing problems (the original formulation of the Standard Model contained neutrinos with zero mass, which we know for a fact not to be longer true – however this was hardly a prediction, it simply accommodated what was known about neutrinos back then and extending the model to accommodate massive neutrinos requires minor adjustments).
This indicates that observing a neutron to antineutron interaction necessitates the discovery of a new interaction mediated by a new particle or particles! Something has to carry out the transaction that permits the transformation to take place. Perhaps it would be surprising, or perhaps it would have been foreseen among the plethora of post-Standard Model hypotheses. However, the most crucial truth is that we would have empirically verified for the first time, beyond a shadow of a doubt, that the Standard Model is incorrect.
If you’re interested in particle physics, you’ve probably heard ad nauseam that the Standard Model is flawed, which I agree with. However, the term “incompleteness” usually refers to matters about which the Standard Model is silent, rather than genuine conflicts between theory and experiment. Even dark matter cannot be used to prove that such tension exists, because the evidence, while convincing, is all astronomical rather than microscopical. As a result, observing neutrons to antineutrons would certainly be a significant step forward in our knowledge of fundamental physics.