As the initial Friedmann equation approaches its 99th birthday, it continues to be the only equation that adequately describes our whole universe.
Share Is it possible to describe the whole history of the universe with only one equation? on the network LinkedIn
It’s quite simple to come to a conclusion based on what you’ve observed so far in science. However, projecting what you know — in the location where it’s been well-tested — to a place that’s beyond your theory’s demonstrated validity poses a significant risk. Newtonian physics, for example, works perfectly until you go down to extremely small distances (where quantum mechanics kicks in), get close to a very high mass (where general relativity kicks in), or get close to the speed of light (when general relativity kicks in) (when special relativity matters). When it comes to explaining our cosmos within the context of our current cosmological framework, we must be cautious.
As time passes, the cosmos as we know it expands, cools, and becomes clumpier and less dense. Things appear to be uniform on the biggest cosmic scales; if you placed a box a few billion light-years on a side anywhere inside the observable universe, you’d find the same average density, everywhere, to an accuracy of 99.997 percent. Yet, when it comes to comprehending the universe, including how it changes through time, both in the far future and in the distant past, just one equation is required: the first Friedmann equation. Here’s why that equation, as well as the assumptions that go into extending it to the entire universe, is so strong.

Countless scientific tests of Einstein’s general theory of relativity have been carried out, putting the theory under some of the most rigorous limitations ever imposed by humanity. Einstein’s initial answer was for the weak-field limit around a single mass, such as the sun, which he successfully applied to our Solar System. Following that, a few of exact answers were immediately discovered. (Credit: T. Pyle, Caltech/MIT, LIGO scientific partnership)
Going all the way back to the beginning of the narrative, Einstein proposed his general theory of relativity in 1915, soon displacing Newton’s law of universal gravitation as the main gravity theory. Unlike Newton’s theory, which proposed that all masses in the cosmos instantly attracted one another by an infinite-ranged “activity at a distance,” Einstein’s idea was significantly different, even in concept.
Instead of serving as an immutable background for people to live and move in, space became intimately linked to time, as the two were knitted together in a fabric known as spacetime. Nothing could go faster through spacetime than light, and the quicker you traveled through space, the slower you traveled through time (and vice versa). The fabric of spacetime curved whenever and wherever any type of energy was present, with the amount of curvature being precisely connected to the universe’s stress-energy level at that place.
In other words, matter and energy were informed how to flow through spacetime by its curvature, while spacetime was told how to curve by the presence and distribution of matter and energy.

In 2017, a portrait of Ethan Siegel was shown on the hyperwall of the American Astronomical Society, along with the first Friedmann equation in contemporary notation. The expansion rate of the cosmos (squared) is on the left, while all kinds of matter and energy, including spatial curvature and a cosmological constant, are on the right. (Photo by Harley Thronson/Perimeter Institute)
Einstein’s laws give a very powerful framework for us to operate inside within general relativity. But it’s also extremely difficult: only the simplest of spacetimes can be solved numerically rather than accurately. The first exact solution was obtained in 1916 by Karl Schwarzschild for a nonrotating point mass, which we now refer to as a black hole. Your equations will become unsolvable if you decide to add a second mass to your universe.
There are, nevertheless, a plethora of exact answers known to exist. One of the first was proposed by Alexander Friedmann in 1922: If the universe were uniformly filled with some sort(s) of energy — matter, radiation, a cosmological constant, or any other form of energy you can think of — and the energy is distributed evenly in all directions and in all locations, then his equations would provide an exact solution for spacetime’s evolution.
Surprisingly, he discovered that the solution was fundamentally unstable over time. If your universe started out in a static condition and was filled with this energy, it would inexorably constrict until it collapsed into a singularity. The third possibility is that the cosmos expands, despite the gravitational influences of all the various types of energy acting against it. The project of cosmology was suddenly placed on a sound scientific platform.

While matter and radiation grow less dense as the universe expands due to its larger volume, dark energy is a type of energy that is fundamental to space. The density of dark energy remains constant as new space is produced in the expanding cosmos. (Credit: E. Siegel/Beyond the Galaxy)
The importance of the Friedmann equations — particularly the first Friedmann equation — for current cosmology cannot be emphasized. It’s possible that the most important discovery in all of physics was a mathematical concept: the differential equation.
In physics, a differential equation is an equation that starts with an initial state and has characteristics that you pick to best reflect the system you have. Do you have any particles? Give us their locations, momenta, masses, and other attributes of interest, and we’ll take care of the rest. The strength of the differential equation is that it shows you how your system will develop to the next moment based on the conditions it started with. Then, using the new locations, momenta, and other characteristics you’ve derived, you can plug them into the same differential equation, which will predict how the system will develop until the next moment.
Differential equations inform us how to develop any physical system forward or backward in time, from Newton’s laws to the time-dependent Schrödinger equation.

The relationship between redshift and distance for extragalactic objects in our universe will be determined by the expansion rate today, as well as the types of matter and energy that exist within your universe. (Credit: Ned Wright/Betoule et al. (2014))
However, there is a limit: you can only play this game for so long. You’ve extrapolated beyond the range where your approximations are viable when your equation no longer represents your system. The contents of your universe must remain constant in order to solve the first Friedmann equation. There are no transformations allowed from one species of energy to another, and matter remains matter, radiation remains radiation, a cosmological constant remains a cosmological constant, and a cosmological constant remains a cosmological constant.
Your universe must also stay isotropic and homogenous. These equations no longer apply if the cosmos takes a favored path or becomes too nonuniform. It’s enough to make you wonder whether our knowledge of how the universe evolves is flawed in some way, or if we’re making an unfounded assumption: that perhaps this one equation, which tells us how the world expands through time, isn’t as reliable as we think.

With the expansion of the cosmos expanded out, this excerpt from a structure-formation simulation reflects billions of years of gravitational growth in a dark matter-rich universe. Despite the fact that the cosmos is expanding, the individual, bound objects inside it are not. Their sizes, on the other hand, might be affected by the growth; we don’t know for sure. ((Credit: Ralf Kahler and Tom Abel (KIPAC)/Oliver Hahn)
This is a dangerous enterprise since science requires us to constantly question our preconceptions. Is there a frame of reference that you prefer? Do galaxies revolve in a clockwise direction more often than in a counterclockwise direction? Is there proof that quasars only exist at redshifts that are multiples of a certain number? Is the cosmic microwave background radiation’s spectrum different from that of a blackbody? Are there structures in the cosmos that are too big to explain in a uniform universe?
These are the kinds of assumptions that we constantly evaluate and test. While many bold claims have been made on these and other fronts, the truth is that none of them have stood up to scrutiny. The only noteworthy frame of reference is one in which the Big Bang’s residual light seems to be uniform in temperature. Left-handed galaxies are just as common as right-handed galaxies. The redshifts of quasars are unquestionably not quantized. The cosmic microwave background’s radiation is the most perfect blackbody we’ve ever measured. Furthermore, the enormous quasar groupings we’ve seen are most likely just pseudo-structures, not gravitationally tied together in any significant way.

On broader cosmic scales than expected, certain quasar groups appear to be grouped and/or aligned. The Huge Large Quasar Group (Huge-LQG) is the biggest of them all, with 73 quasars spanning up to 5-6 billion light-years. However, it might just be a pseudo-structure. (Credit: ESO/M. Kornmesser)
If, on the other hand, all of our assumptions hold true, running these equations forward or backward in time as long as we want becomes a simple exercise. All you have to know is this:
- what is the current rate of expansion of the cosmos
- what are the many forms and densities of matter and energy in use today
That’s all there is to it. You may extrapolate ahead or backward as far as you want with only that knowledge, allowing you to know what the observable universe’s size, expansion rate, density, and a variety of other characteristics were and will be at any given point.
Our universe today, for example, is made up of around 68 percent dark energy, 27 percent dark matter, 4.9 percent normal matter, 0.1 percent neutrinos, 0.01 percent radiation, and insignificant quantities of everything else. We can discover how the cosmos expanded in the past and will grow in the future by extrapolating that both backward and forward in time.
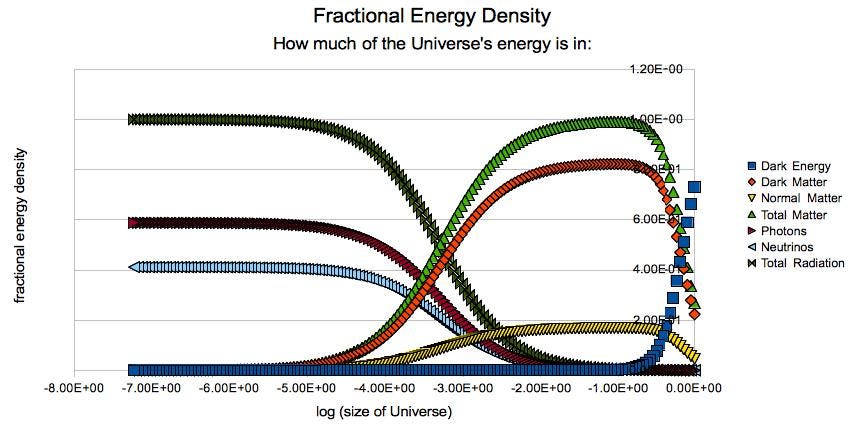
At various eras in the past, the relative prominence of various energy components in the cosmos. Note that when dark energy reaches a value approaching 100% in the future, the universe’s energy density (and, therefore, the expansion rate) will asymptote to a constant, but will continue to decrease as long as matter exists in the cosmos. (Credit: E. Siegel)
But are the conclusions we’d reach sound, or are we relying on unfounded assumptions? Here are some occurrences that have happened throughout the universe’s history that might throw a kink in our assumptions:
- Stars exist, and as they burn up their fuel, part of their rest-mass energy (normal matter) is converted into radiation, altering the universe’s composition.
- Gravitation occurs, and the production of structure results in an inhomogeneous cosmos with substantial density disparities across regions, especially where black holes exist.
- When the universe is young and hot, neutrinos behave as radiation, but once the cosmos has expanded and cooled, they behave as matter.
- The cosmos must have been filled with the equivalent of a cosmological constant very early in the universe’s existence, which must have decayed away (signifying the end of inflation) into the matter and energy that populates the universe today.
Surprisingly, only the fourth of them plays a significant part in changing the course of our universe’s history.

When inflation occurs, quantum fluctuations are spread over the cosmos, and when inflation stops, density fluctuations result. This results in the large-scale structure of the cosmos today, as well as the temperature changes seen in the CMB. These kinds of new predictions are crucial for proving the viability of a suggested fine-tuning process. (Credit: E. Siegel; ESA/Planck and the DOE/NASA/NSF Interagency Task Force on CMB research)
The explanation for this is simple: we can measure the effects of the others and observe that they only have a 0.001% or lower impact on the expansion rate. Only a small proportion of the mass of stars, which is itself a small fraction of normal matter, is ever transformed into radiation, which causes a slow and low-magnitude shift in the expansion rate. The effects of gravity have been carefully investigated and quantified (including by me! ), and while they can have a minor effect on the pace of expansion on small cosmic scales, the global contribution has no effect on the overall expansion rate.
Similarly, we can account for neutrinos to the extent that their rest masses are well understood, so there’s no uncertainty there. The only problem is that if we travel back far enough in time, there is a sudden shift in the universe’s energy density, and abrupt changes, rather than smooth and continuous ones, are what might completely invalidate our usage of the first Friedmann equation. If there is a component of the cosmos that rapidly decays or transitions into something else, that is the only thing we know of that may cause our assumptions to be challenged. That will be the point at which invoking the Friedmann equation will fail.
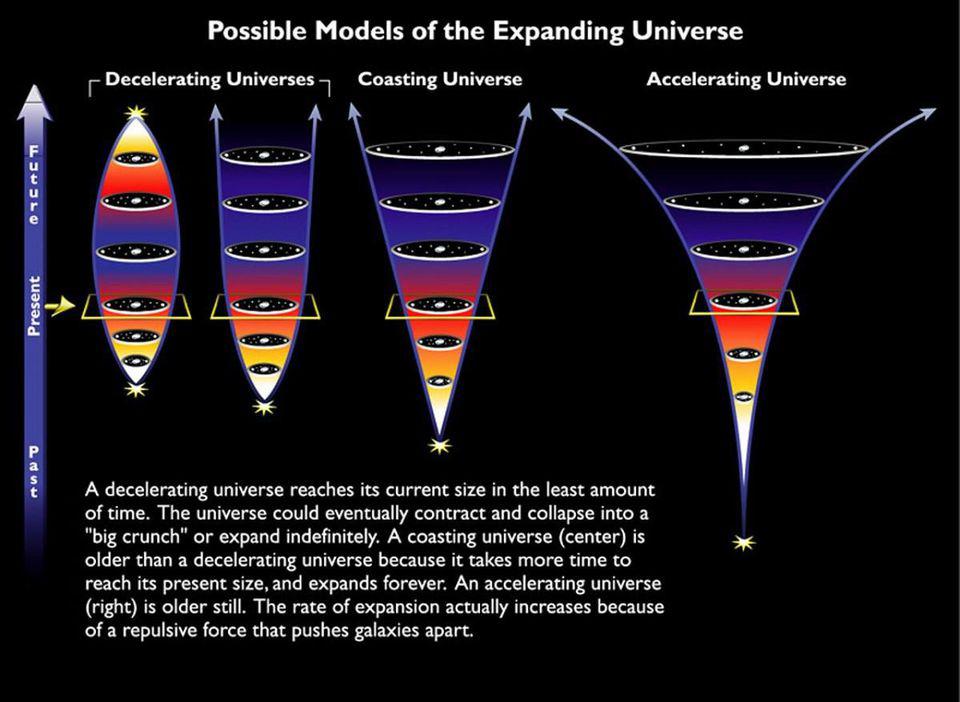
The various conceivable outcomes for the cosmos, with our current, speeding fate depicted on the right. After a sufficient amount of time has passed, the acceleration will isolate every bound galaxy or supergalactic structure in the universe, as all other structures speed irreversibly away. We can only deduce the presence and qualities of dark energy by looking back in time, which requires at least one constant, but the consequences for the future are far greater. (Credit: NASA & ESA)
Conclusions concerning how the cosmos will operate in regimes outside our observations, measurements, and experiments are exceedingly difficult to reach. We can only rely on how well-known and well-tested the underlying theory is, take the measurements and observations that we can, and draw the best conclusions we can based on what we know. But we must constantly remember that the universe has shocked us at several crossroads in the past and will most certainly do so again. When it occurs, we must be prepared, and part of that preparation includes being willing to question even our most strongly held beliefs about how the universe works.
The Friedmann equations, particularly the first Friedmann equation, which connects the expansion rate of the universe to the sum total of all the distinct types of matter and energy inside it, have been known for 99 years and applied to the cosmos for almost as long. It’s showed us how the cosmos has grown through time, and it’s given us the ability to foresee our final fate, even in the far future. Can we be assured, however, that our conclusions are correct? Only to a certain degree of certainty. We must always be cautious of even the most persuasive findings, regardless of the limits of our evidence. Beyond the known, our best guesses are just that: guesses.


