Four new levels of sensitivity to neutrinoless double-beta decay, a process whose presence would imply that neutrinos are their own antiparticles, have been established in four tests.
At high-energy particle accelerators, the hunt for physics beyond the standard model—our current best explanation of fundamental particles and their interactions—is a primary priority. However, through a process known as neutrinoless double-beta (0v) decay, researchers are looking for new physics in the nucleus’ “low-energy” surroundings. This hypothetical decay would demonstrate that neutrinos are their own antiparticles and that nature violates a basic law: the conservation of lepton number. It would also explain neutrinos’ lightness. New lower bounds on the decay’s half-life have been reported by four experimental teams [1–4], all of which exceed 1025 years. Several of these trials should reach the 1026 level soon, allowing a fifth experiment [5] to catch up. These new findings prompt a debate about why detecting 0 decay is important and what physicists can learn if the tests become more sensitive.
Neutrinos are distinguished by their incredibly low mass. The particles are around 106 times lighter than the next lightest fermion, the electron, and exist in three different mass states. This large disparity shows that the genesis of neutrino mass is distinct from that of all other fermions, implying that physics beyond the standard model is involved. The neutrinos are Majorana particles, which means they are their own antiparticles, according to most such extensions of the model. According to these hypotheses, the masses of light neutrinos are inversely related to a large mass scale established by unknown particles.
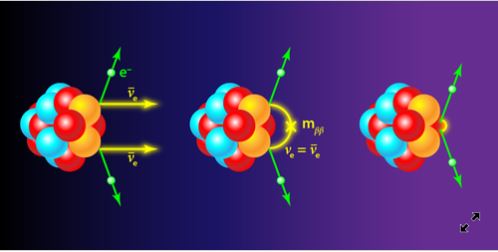
If neutrinos are Majorana particles, they defy the conservation of lepton number (the quantum number ascribed to all leptons, which is 1 for electrons and neutrinos and 1 for their antiparticles). Two neutrons are transformed into two protons plus two electrons and two antineutrinos in the process of two-neutrino beta decay (Fig. 1, left), which is allowed in specific isotopes. Because electrons and antineutrinos have opposing lepton numbers, the lepton number is conserved. If neutrinos are Majorana particles, however, double-beta decay can occur without the emission of antineutrinos, resulting in a two-fold change in the lepton number.
This neutrinoless process could be mediated by a number of methods. They entail the formation and annihilation of a virtual Majorana neutrino (Fig. 1, middle) or a new heavy particle (Fig. 1, right). The decay rate is proportional to the square of a mass termed m, which is a weighted average of the masses of the three neutrino mass states if nature picks the first scenario (virtual Majorana neutrinos). The relationship between the decay rate and neutrino masses becomes more convoluted if nature favours the second alternative (heavy particles). However, discovering the decay, regardless of the mechanism that causes it, would indicate that neutrinos are Majorana particles and that new particles exist that allow for lepton number nonconservation. The fact that the number of leptons isn’t conserved may also push scientists in the direction of an explanation for the observed asymmetry in matter and antimatter.
The decay half-life (the inverse of the decay rate) is determined in roughly the same method in all four experiments: by monitoring a large number of atoms of a certain double-beta decay isotope and looking for a peak in the two-electron energy. (In 0 decay, the two electrons carry away the entire decay energy, which is equal to the difference in mass between the starting and final nuclei.) The experiments differ in terms of the isotopes used and how the electron energies are measured. The MAJORANA Demonstrator [2] at the US’s Sanford Underground Research Facility and the GERDA [1] at Italy’s Gran Sasso underground laboratory both look for decays in materials enriched in germanium-76. EXO-200 [4] studies liquid xenon enhanced with xenon-136 at the Waste Isolation Pilot Plant in the United States. Finally, at Gran Sasso, CUORE [3] investigates TeO2 crystals produced of natural tellurium, of which 34% is the double-beta decay isotope tellurium-130.
The best half-life limits to date are from GERDA, which currently claims a lower limit of 81025 years [1], and from KamLAND-Zen, a fifth experiment at the Kamioka Observatory in Japan, which employs xenon-136 and obtained a limit of 1.071026 years in 2016 [5]. The limitations given by EXO-200 (1.81025 years [4]), MAJORANA (1.91025 years [2]), and CUORE (1.31025 years [3]) last month and today are very near.
Why did you pick one isotope over the other? The nuclear wave function and the density of final electron states determine the anticipated decay rate for a specific isotope. When compared to germanium-76, the heavier isotopes (xenon-136 and tellurium-135) give a sixfold increase in electron-state density. In germanium-76, however, the contribution from the nuclear wave function is projected to be the biggest [6]. After all is said and done, the three isotopes have roughly equal sensitivity to m, or the physics of heavy new particles, with the heavier two maybe having a little advantage.
Finally, exposure, which is the product of the amount of active isotope and the measuring duration, is the most critical factor in sensitivity. Another important feature is the capacity to spot a faint electron signal amid a sea of noise. To eliminate “false” counts, the tests usually limit the search to energies in a restricted range near the decay energy. The higher a detector’s energy resolution, the fewer erroneous counts it can eliminate. Although the CUORE experiment has more exposure than the germanium trials, its resolution is worse. As a result, the GERDA half-life limit is slightly larger than that of CUORE, which, like MAJORANA, has produced “zero-background” conditions in its region of interest. The xenon tests had the most exposure but the worst resolution of all. That’s why they’ve come up with limits that are comparable to those found in the germanium studies so far.
With higher sensitivities, the investigations might have a better probability of really identifying 0 decay. Other tests’ constraints on m show that it could be greater than 10 meV. Estimates [6] show that a discovery with an experimental sensitivity of 5– 81026 years is achievable if it is as massive as 50 meV and the decay is mediated by virtual Majorana neutrinos. If m is closer to 10 meV, however, a sensitivity of 1– 21028 years will be required to detect the decay. Some of the experiments may be able to achieve the first of these objectives if they are simply allowed to run. To achieve the second target, however, the detectors will need a 100-fold increase in sensitivity, which will necessitate a ton or more of active material and superior background-elimination procedures. (See, for example, the Focus piece from March 26, 2018.) Experiments with no background provide the optimum sensitivity scaling as exposure increases. However, with that much content, achieving zero background will be a technical challenge that would require major money.
Larger detectors with all three isotopes have already formed collaborations. But, when one measurement isn’t clearly superior than the other, do we need so many tests dedicated to it? The first is that identifying the decay would necessitate a textbook rewrite—lepton number is not preserved, and neutrinos are Majorana—so supplementary experiments are required to corroborate such a significant result. There is, however, another justification for having many projects. We want to learn more about the degradation if we notice it. Is it propelled by light particles or by heavy particles? If the latter, what are the new particles’ properties? If we can estimate the decay rates of multiple isotopes, these problems become easier to answer. Furthermore, quantifying the single-electron energy spectrum and other features of the decay would provide a more definitive knowledge of the mechanism for lepton number violation. Researchers will be able to better decide how to conduct these more difficult measures if they have a set of trials dedicated to the same subject.
References
- “Improved Limit on Neutrinoless Double-Decay of 76Ge from GERDA Phase II,” M. Agostini et al. (GERDA Collaboration), Phys. Rev. Lett. 120, 132503 (2018).
- “Search for Neutrinoless Double-Decay in 76Ge with the Majorana Demonstrator,” Phys. Rev. Lett. 120, 132502 (C. E. Aalseth et al., MAJORANA Collaboration) (2018).
- “First Results from CUORE: A Search for Lepton Number Violation via 0v decay of 130Te,” Phys. Rev. Lett. 120, 132501. C. Alduino et al. (CUORE Collaboration), “First Results from CUORE: A Search for Lepton Number Violation via 0v decay of 130Te,” Phys. Rev. Lett. 120, 132501. (2018).
- “Search for Neutrinoless Double-Beta Decay with the Upgraded EXO-200 Detector,” Phys. Rev. Lett. 120, 072701 (J. B. Albert et al., EXO-200 Collaboration) (2018).
- “Search for Majorana Neutrinos Near the Inverted Mass Hierarchy Region with KamLAND-Zen,” Phys. Rev. Lett. 117, 082503 (A. Gando et al., KamLAND-Zen Collaboration) (2016).
- “Status and Future of Nuclear Matrix Elements for Neutrinoless Double-Beta Decay: A Review,” Rep. Prog. Phys. 80, 046301. J. Engel and J. Menéndez, “Status and Future of Nuclear Matrix Elements for Neutrinoless Double-Beta Decay: A Review,” Rep. Prog. Phys. 80, 046301. (2017).