|
Getting your Trinity Audio player ready...
|
Professor Costas Vayenas and his colleagues Dionysios Tsousis and Dimitrios Grigoriou show how applying special relativity to neutrino travel at fm distances leads to Bohr type models with relativistic gravity as the attractive force.
The Standard Model (SM) of particle physics has served as the foundation for defining the structure and composition of matter for the last fifty years. According to the SM, protons and neutrons, which are components of atomic nuclei and belong to the hadron family of composite particles, are made up of fundamental particles called quarks that are held together by a force known as the Strong Force. (1) No quarks have ever been separated and analyzed individually, and their masses are believed to be equivalent to baryon masses, i.e. on the order of 1 GeV/c2. These masses are 100 billion times (10,11) greater than the masses of neutrinos (10-1 to 10-3 eV/c2) (2), which are by far the lightest and most abundant particles in our Universe.
With increasing speed, inertial and gravitational mass rise.
Einstein’s Relativity Theory (both special (SR) (3,4) and general (GR) (5)) is one of the most impressive scientific discoveries in human history. SR has been proven experimentally hundreds of times, while GR has also been confirmed multiple times. Most confirmations are based on macroscopic systems, and only lately (6) has the incredible strength of SR and GR been proved within hadrons, deep into the femtocosmos of the lightest fundamental particles, namely neutrinos.
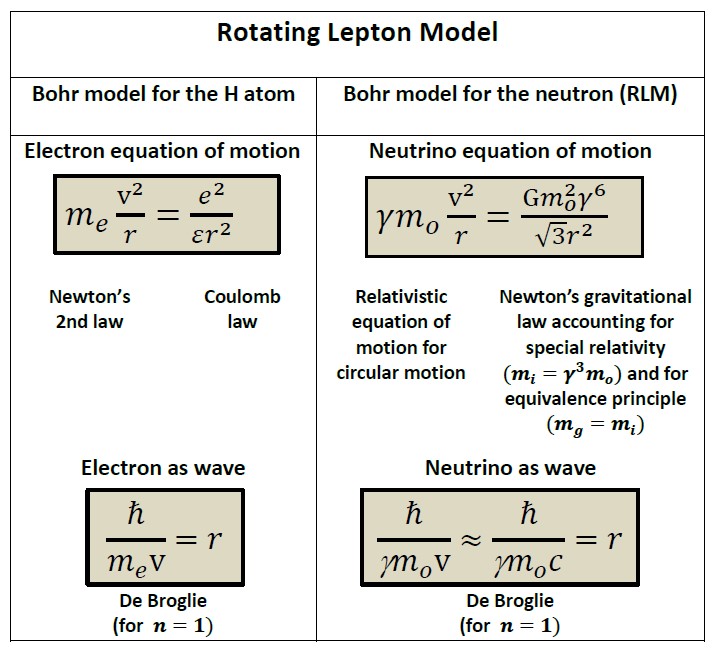
The key aspects of SR are space contraction, time dilation, and mass increase with particle speed as the particle speed with respect to an observer at rest with the center of rotation approaches the speed of light c and therefore the Lorentz factor, given as = (1 – v2 / c2) –1/2, approaches infinity.
Thus, when three particles rotate symmetrically on a cyclic trajectory with their gravitational pull, FG, acting as the centripetal force, FG might become remarkably powerful. This is because SR states that a particle with rest mass mo has a relativistic mass mo (3,4) and a longitudinal inertial mass 3mo, which is equivalent to its gravitational mass 3mo according to the equivalence principle (6,7). (7,8) As a result, using Newton’s gravitational law’s concept of gravitational mass, the following is true:
Gm2o6 / (3r2) = FG (1)
r denotes the rotating radius. To calculate r and, use the de Broglie equation from Quantum Mechanics:
mover = n (2)
This is used to calculate n=1 and mo43.7 meV/c2, which are calculated (6,8) from Superkamiokande observations, (2) that r0.63 fm and 7.163.109, and so 61.35.1059. As a result, the rotational speed is extremely near to c, and the gravitational force is 59 orders of magnitude more than the standard nonrelativistic Newtonian force, according to equation (1)! (See Figure 1) This force is 8.104 N, which is equivalent to the weight of 100 individuals on Earth.
Neutrinos, Quarks, and Hadrons Gain Relativistic Mass
In addition to increasing gravitational attraction by 61059 times, special elativity boosts the mass of the three revolving neutrinos by 7.168.109 times, causing the composite particle mass to grow from 3(43.7 meV/c2) to the neutron mass of 939.565 MeV/c2 (Fig. 1). If the composite particle mass, 3mo, is that of a neutron (939.565 MeV/c2), then the rest mass, mo, of each revolving particle is that of the heaviest neutrino eigenmass, (9) i.e. 43.7 meV/c2, which is consistent with the Superkamiokande measurement of the heaviest neutrino mass. (2) As a result, special relativity demonstrates that quarks are relativistic neutrinos and that the neutrino gravitational mass, 3mo, is massive, on the order of the Planck mass (c/G)1/2 = 21.7 mg per neutrino! In combination with equation (2), this indicates that the gravitational force of equation (1) equals the strong force, c/r2, which is 137 times greater than the electrostatic force of a positron-electron pair at the same distance. (1)
Minimization of energy and calculation of Hadron mass
The RLM demonstrates that increasing the Lorentz factor leads to increased composite particle stability by minimizing –5moc2, which is the potential energy of the rotating neutrino triad (8) and, at the same time, increasing the Lorentz factor and thus increasing the produced hadron mass m = 3mo = 313/12 (mP1mo2)1/3, where mP1 is the Planck mass (=(c/G)1/2 = 1.22.1028 eV/ Surprisingly, this simple calculation yields a mass value that varies by less than 1% from the observed neutron mass of 939.565 MeV/c2.

Neutrinos are generally known to occur in three distinct “flavors,” namely electron neutrinos, muon neutrinos, and tau neutrinos. These flavors are created by combining neutrinos from the three mass types (or mass eigenstates), namely m3 mass neutrinos (the heaviest), m2 mass neutrinos, and m1 type neutrinos (the lightest) for the Normal Hierarchy. Using equation (1) and the measured hadron masses, we calculated the composite particle mass values presented in Figure 2. The agreement with the experimental composite mass values is greater than 2%. Alternatively, the experimental hadron or boson masses may be used to calculate the three neutrino masses. The agreement with the experimental values observed at Superkamiokande (2) is within 5%.
Unification of the military forces
The fact that the gravitational Newton-Einstein equation (1) fits the observed mass values of hadrons so well suggests that, when special relativity is taken into account, gravity is sufficient to explain the strong force. The similarly excellent match to the measured mass values of W, Z0, and H bosons demonstrates that relativistic gravity may likewise be used to explain the weak force. Indeed, at the limit of big, one gets FG = Gm2 P1 / r2 = G(c / G) / r2 = c/r2, which is the strong force value. (1) Similarly, with the weak force, one gets FG = c/r2. As a result, both the strong and weak forces have been united with Newtonian gravity (=1) in the RLM through equation (1). (10,12)
In short, the RLM indicates that our known Universe is the result of a mixture of neutrinos, electrons, positrons, Einstein’s relativity, and the dual wave-particle duality of matter, as defined by the de Broglie equation of quantum mechanics. (12,13)



